-光と光学に関連する用語の解説サイト-

y=sinxとy=cosxに囲まれた部分の回転体の体積

◆第問目！

【 難易度 ★★ 】
　\({y=\sin x\hspace{2pt},}\)\({\hspace{3pt}y= \cos x\hspace{2pt}}\)\({\left(\frac{\pi}{4} \leqq x \leqq \frac{5}{4}\pi\hspace{1pt}\right)}\) に囲まれた部分を\({\hspace{1pt}x}\)軸の周りに回転させた回転体の体積を求めよ

\({y=\sin x\hspace{2pt},}\)\({\hspace{3pt}y= \cos x\hspace{2pt}}\)のグラフを描くと、回転する部分が\({x\hspace{1pt}}\)軸をまたいでいることが分かります。

\({x\hspace{1pt}}\)軸をまたいでいる部分の回転体の体積を求めるときは、\({\hspace{1pt}y< 0 \hspace{2pt}}\)となる箇所を\({\hspace{1pt}x\hspace{2pt}}\)軸で折り返した部分を含めて回転体を考えます。

【解答のポイント】

\({y=\sin x\hspace{2pt},}\)\({\hspace{3pt}y= \cos x\hspace{2pt}}\)のグラフを描くと、回転する部分が\({x\hspace{1pt}}\)軸をまたいでいることが分かります。

\({x\hspace{1pt}}\)軸をまたいでいる部分の回転体の体積を求めるときは、\({\hspace{1pt}y< 0 \hspace{2pt}}\)となる箇所を\({\hspace{1pt}x\hspace{2pt}}\)軸で折り返した部分を含めて回転体を考えます。

区間\({\hspace{1pt}[a,b]\hspace{2pt}}\)において関数\({\hspace{1pt}f(x) \geqq g(x) \geqq 0 \hspace{2pt}}\)であるとき、この2つの曲線と\({\hspace{1pt}x=a,x=b\hspace{2pt}}\)によって囲まれる部分を\({\hspace{1pt}x\hspace{2pt}}\)軸の周りに回転させた回転体の体積は

$$\hspace{10pt}{V= \pi \int_a^b (f(x))^2 \hspace{1pt}dx - \pi \int_a^b (g(x))^2 \hspace{1pt}dx}\hspace{10pt}$$

と求められます。

【解答】

まず、\({y=\sin x\hspace{2pt},}\)\({\hspace{3pt}y= \cos x\hspace{2pt}}\)の交点の座標は $${x = \frac{\pi}{4}\hspace{1pt},\hspace{1pt}\frac{5}{4}\pi}$$ となります。

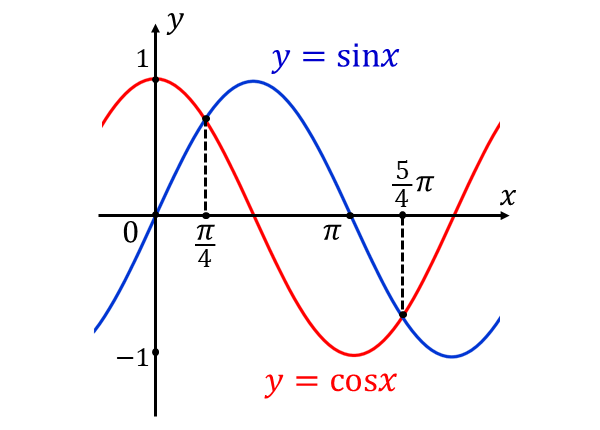
\({y=\sin x\hspace{2pt},}\)\({\hspace{3pt}y= \cos x\hspace{2pt}}\)のグラフを描くと以下のようになります。 y=sinx,y=cosxに囲まれた部分の図

ここで、上図から\({\hspace{1pt}y=\sin x\hspace{2pt},}\)\({\hspace{3pt}y= \cos x\hspace{2pt}}\)は\({\hspace{1pt}x\hspace{2pt}}\)軸をまたいでいるため、\({\hspace{1pt}y< 0 \hspace{2pt}}\)となる箇所を\({\hspace{1pt}x\hspace{2pt}}\)軸で折り返した部分を含めて回転体を考えます。

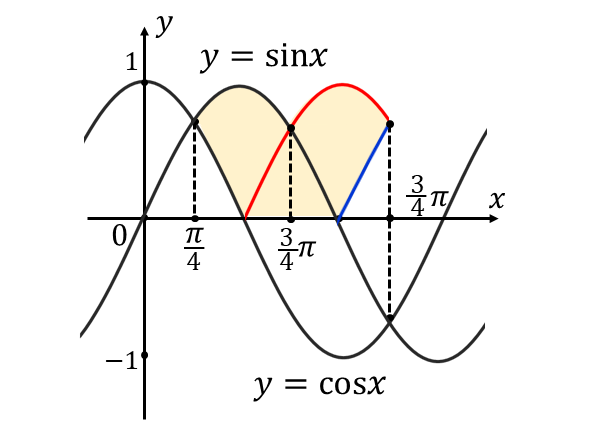
以下に、\({\hspace{1pt}y< 0 \hspace{2pt}}\)となる箇所を\({\hspace{1pt}x\hspace{1pt}}\)軸で折り返した部分を含めた図を示します。図中の黄色に塗られた部分が回転すると考えて積分します。 y=sinx,y=cosxに囲まれた部分のうち、x軸をまたぐ部分を折り返した図

上図から、回転する部分は\(\displaystyle{\hspace{1pt}x=\frac{3}{4}\pi\hspace{2pt}}\)で対称となっていることが分かります。

そのため、区間\(\displaystyle \hspace{1pt}\left[\frac{\pi}{4},\frac{3}{4}\pi \right]\hspace{1pt}\)で求められる体積を2倍して全体の体積を求めます。

以上から、回転体の体積は以下のように求められます。

$$ \begin{aligned} \hspace{10pt}& 2 \left( \pi \int_{\frac{\pi}{4}}^{\frac{3}{4}\pi} \sin^2 x \hspace{1pt}dx - \pi \int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \cos^2 x \hspace{1pt}dx \right) \\[1.3em] & = 2 \pi \left(\int_{\frac{\pi}{4}}^{\frac{3}{4}\pi} \frac{1-\cos 2x}{2} \hspace{1pt}dx - \int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \frac{1+\cos 2x}{2} \hspace{1pt}dx \right) \\[1.3em] & = \pi \left(\int_{\frac{\pi}{4}}^{\frac{3}{4}\pi} (1-\cos 2x)\hspace{1pt}dx - \int_{\frac{\pi}{4}}^{\frac{\pi}{2}}(1+\cos 2x)\hspace{1pt}dx \right) \\[1.3em] & = \pi \left (\left[ x -\frac{1}{2}\sin 2x \right]_{\frac{\pi}{4}}^{\frac{3}{4}\pi} -\left[ x +\frac{1}{2}\sin 2x \right]_{\frac{\pi}{4}}^{\frac{\pi}{2}} \right)\\[1.3em] & = \pi \left (\frac{3}{4}\pi - \frac{\pi}{4} -\frac{1}{2}(-1-1) - \left(\frac{\pi}{2} - \frac{\pi}{4}\right) -\frac{1}{2}(0-1)\right)\hspace{10pt}\\[1.3em] & = \pi \left (\frac{1}{4}\pi +\frac{3}{2}\right)\\[1.3em] & =\frac{(\pi + 6)\pi}{4}\\[1.3em] \end{aligned} $$

と求められます。

(上記の計算過程には半角の公式 $$\displaystyle{\sin^2 x = \frac{1-\cos 2x}{2}}$$ $$\displaystyle{\cos^2 x = \frac{1+\cos 2x}{2}}$$を使用しています。)

　【出題範囲】　　　【難易度】


　



Copyright (c) 光学技術の基礎用語 All Rights Reserved.