-光と光学に関連する用語の解説サイト-

媒介変数表示された楕円の面積

◆第問目！

【 難易度 ★★ 】
　\({x=a \cos \theta\hspace{2pt}}\)と\({\hspace{2pt}y=b \sin \theta\hspace{2pt}}\)\({(\hspace{1pt}a,b>0\hspace{2pt},0 \leqq \theta \leqq 2\pi\hspace{1pt})}\) に囲まれる面積を求めよ

本問は媒介変数表示された楕円の面積を求める問題です。

【解答のポイント】

本問は媒介変数表示された楕円の面積を求める問題です。

【解答】

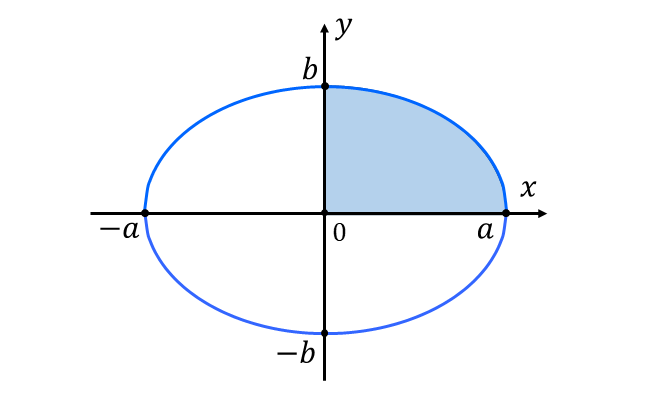
問題の楕円を図に描くと以下のようになります。 媒介変数表示された楕円の面積を求める問題

楕円は\({x}\)軸と\({y}\)軸に関して対称であるため、\({x \geqq 0\hspace{2pt},}\)\({\hspace{1pt}y \geqq 0\hspace{2pt}}\)の部分の面積を求めてから、4倍して全体の面積を求めます。

ここで、上図の積分区間は\({\hspace{1pt}[0,a]\hspace{2pt}}\)となりますが、\({x= a \cos \theta \hspace{2pt}}\)から変数\({x}\) の範囲に対応する 変数\({\theta}\) の範囲を求めると、以下のようになります。

\({x}\) \({0 \to a}\)
\({\theta}\) \(\displaystyle{\frac{\pi}{2} \to 0}\)

また、\({x=a \cos \theta\hspace{2pt}}\)を\({\hspace{1pt}\theta\hspace{2pt}}\)に関して微分すると\(\displaystyle{\hspace{1pt}\frac{dx}{d\theta}=-a\sin \theta\hspace{2pt}}\)となることから、\({\hspace{1pt}dx=-a \sin \theta d\theta\hspace{2pt}}\)と表せます。

以上から、図の楕円の4分の1の面積は以下のように求められます。

$$ \begin{aligned} \hspace{10pt}& \int_{0}^{a} y \hspace{1pt}dx \\[1em] & = \int_{\frac{\pi}{2}}^{0} b\sin \theta \cdot (-a \sin \theta)\hspace{1pt}d\theta\\[1em] &= ab \int_{0}^{\frac{\pi}{2}} \sin^2 \theta \hspace{1pt}d\theta\\[1em] & = ab \int_{0}^{\frac{\pi}{2}} \frac{1-\cos 2\theta}{2} \hspace{1pt}d\theta \\[1em] & = \frac{ab}{2}\left[\theta - \frac{1}{2}\sin 2\theta \right]_{0}^{\frac{\pi}{2}} \\[1em] & = \frac{ab}{2} \cdot \frac{\pi}{2} \\[1em] & = \frac{ab}{4} \pi \\[1em] \end{aligned} $$

と求められます。

(上記の計算過程には半角の公式 $$\displaystyle{\sin^2 x = \frac{1-\cos 2x}{2}}$$を使用しています。)

したがって、求める面積は $${\frac{ab}{4} \pi \times 4 = ab \pi}$$ となります。

　【出題範囲】　　　【難易度】


　



Copyright (c) 光学技術の基礎用語 All Rights Reserved.