陰関数(2x^2 -2xy + y^2=3)に囲まれた面積

【解答のポイント】

陰関数の面積を求める問題は、まず関数を変形して\({\hspace{1pt}y=\cdots\hspace{2pt}}\)の形に変形します。

次に得られた式を連立させて、グラフの交点を求めます。

最後に、囲まれる範囲において (上側の関数)-(下側の関数) の式を作り、定積分から面積を求めます。

【解答】

まず関数を変形して\({\hspace{1pt}y=\cdots\hspace{2pt}}\)の形に変形します。

$$ \begin{aligned} \hspace{10pt}& 2x^2 -2xy + y^2=3 \\[0.5em] & y^2-2xy + 2x^2 -3 = 0\\[0.5em] \end{aligned} $$

解の公式から $$ \begin{aligned} \hspace{10pt} y &= x \pm \sqrt{x^2 -(2x^2-3)} \\[0.5em] & = x \pm \sqrt{3-x^2} \\[0.5em] \end{aligned} $$

と変形することができます。

ここで、以下の二式を連立させて交点を求めます。 $$ \begin{aligned} y &= x + \sqrt{3-x^2} \hspace{10pt}\cdots(1) \\[0.5em] y &= x - \sqrt{3-x^2} \hspace{10pt}\cdots(2) \\[0.5em] \end{aligned} $$

(1)式と(2)式から\({\hspace{1pt}y\hspace{2pt}}\)を削除すると

すなわち、交点の\({\hspace{1pt}x\hspace{2pt}}\)座標は\({\hspace{1pt}-\sqrt{3}\hspace{1pt},\hspace{1pt}\sqrt{3}\hspace{2pt}}\)となります。

また、\({-\sqrt{3} \leqq x \leqq \sqrt{3}\hspace{2pt}}\)の範囲において、\({\hspace{1pt}x + \sqrt{3-x^2} \geqq x - \sqrt{3-x^2} \hspace{2pt}}\)となります。

(1),(2)式のグラフを描くと以下のようになります。

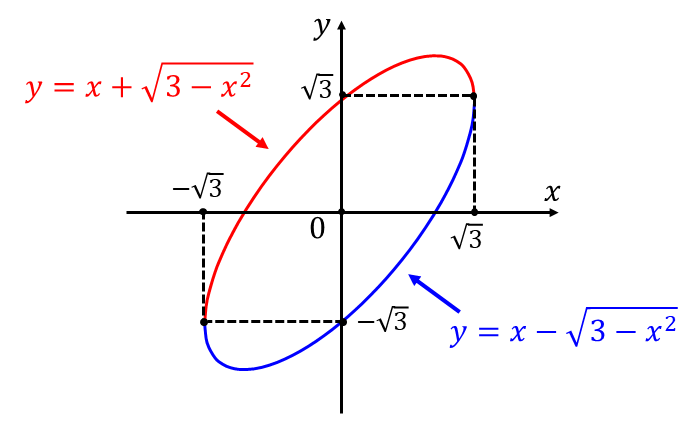
上図から、グラフに囲まれた面積は以下のように求められます。

ここで、\(\displaystyle{\hspace{1pt}\int_{-\sqrt{3}}^{\sqrt{3}} \sqrt{3-x^2} \hspace{1pt}dx\hspace{2pt}}\)は半径\({\hspace{1pt}\sqrt{3}\hspace{2pt}}\)の円の2分の1の面積を表すため

と求められます。