sinxとsin2xに囲まれた面積

【解答のポイント】

まず\({\hspace{2pt}y=\sin x\hspace{2pt}}\)と\({\hspace{1pt}y=\sin 2x\hspace{2pt}}\)の交点を求めるために、二倍角の公式 $${\sin 2 x = 2 \sin x \cos x}$$

を用いて三角方程式を解きます。

積分するためにはグラフの上下関係を調べる必要がありますが、三角関数のグラフの特徴を考えると即座に上下関係が分かります。

【解答】

\({y=\sin x\hspace{2pt}}\)と\({\hspace{1pt}y=\sin 2x\hspace{2pt}}\)の交点を求めます。 $$ \begin{aligned} \sin x - \sin 2x &= 0 \\[1em] \sin x - 2 \sin x \cos x&= 0\\[1em] \sin x(1 - 2 \cos x) &= 0\\[1em] \end{aligned} $$

すなわち \(\displaystyle{\sin x = 0\hspace{2pt}}\)または \(\displaystyle{\cos x = \frac{1}{2}\hspace{2pt}}\)となります。

上式を \({0 \leqq x \leqq \pi\hspace{2pt}}\)の範囲で解くと $${x= 0\hspace{2pt},\hspace{2pt}\frac{\pi}{3}\hspace{2pt},\hspace{2pt}\pi}$$ となります。

ここで、\({y=\sin 2x\hspace{2pt}}\)のグラフの周期は\(\displaystyle{\hspace{2pt}\frac{2 \pi}{2}=\pi\hspace{2pt}}\)となるため、\({y=\sin 2x\hspace{2pt}}\)のグラフは\({\hspace{2pt}y=\sin x\hspace{2pt}}\)を\({\hspace{1pt}x\hspace{2pt}}\)軸方向に\(\displaystyle{\hspace{1pt}\frac{1}{2}\hspace{2pt}}\)倍だけ縮小したものになります。
(三角関数のグラフの周期の性質から\({\hspace{2pt}\sin ax\hspace{2pt}}\)の周期は\(\displaystyle{\hspace{1pt}\frac{2 \pi}{a}\hspace{2pt}}\)となります。)

すなわち、\({\hspace{2pt}y=\sin x\hspace{2pt}}\)と\({\hspace{1pt}y=\sin 2x\hspace{2pt}}\)のグラフは以下のようになります。

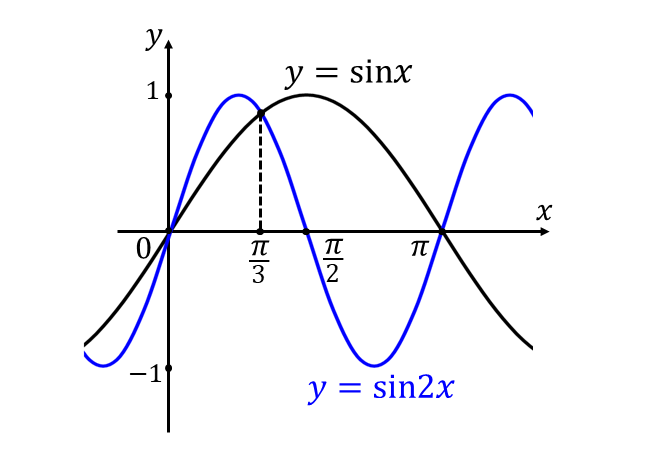
\({0 \leqq x \leqq \pi\hspace{2pt}}\)において、上図の囲まれた面積を求めると、以下のようになります。

【関連するページ】
・三角関数の積分公式

・二倍角の公式

・三角方程式

・三角関数のグラフ