-光と光学に関連する用語の解説サイト-

放物線とx軸で囲まれた面積から定数を求める

◆第問目！

【 難易度 ★ 】
　放物線\(\hspace{2pt}y = -x^2 +3ax\hspace{2pt}\)\(\hspace{2pt}(a > 0)\hspace{1pt}\)と\(\hspace{1pt}x\hspace{1pt}\)軸で囲まれた部分の面積が\(\hspace{1pt}9\hspace{1pt}\)のとき、定数\(\hspace{1pt}a\hspace{1pt}\)を求めよ

積分の計算には、放物線と\(\hspace{1pt}x\hspace{1pt}\)軸に囲まれた面積\(\hspace{1pt}S\hspace{1pt}\)は1/6公式

$${\hspace{10pt}\int_\alpha^\beta (x-\alpha)(x-\beta)\hspace{1pt}dx = -\frac{1}{6}(\beta-\alpha)^3\hspace{10pt}}$$

を用いると簡単に計算できます。

【解答のポイント】
積分の計算には、放物線と\(\hspace{1pt}x\hspace{1pt}\)軸に囲まれた面積\(\hspace{1pt}S\hspace{1pt}\)は1/6公式

$${\hspace{10pt}\int_\alpha^\beta (x-\alpha)(x-\beta)\hspace{1pt}dx = -\frac{1}{6}(\beta-\alpha)^3\hspace{10pt}}$$

を用いると簡単に計算できます。

【解答】
まず、放物線\(\hspace{2pt}y = -x^2 +3ax\hspace{2pt}\)と\(\hspace{1pt}x\hspace{1pt}\)軸の交点の\(\hspace{1pt}x\hspace{1pt}\)座標を求めると $$\begin{aligned} -x^2 +3ax & = 0\\[0.5em] -x(x-3a) &= 0\\[0.5em] \end{aligned} $$ よって、\(x = 0 , 3a\hspace{1pt}\)となります。

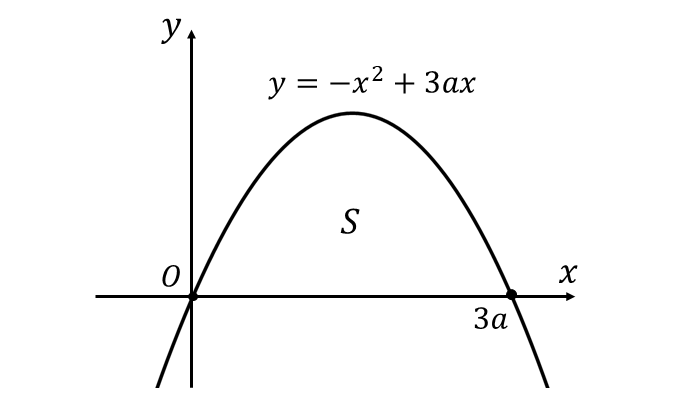
放物線\(\hspace{2pt}y = -x^2 +3ax\hspace{2pt}\)と\(\hspace{1pt}x\hspace{1pt}\)軸で囲まれた部分の面積を作図すると、以下のようになります。 放物線y=-x^2+2axとx軸との面積から定数aを求める問題

放物線と\(\hspace{1pt}x\hspace{1pt}\)軸に囲まれた面積\(\hspace{1pt}S\hspace{1pt}\)は1/6公式

$${\hspace{10pt}\int_\alpha^\beta (x-\alpha)(x-\beta)\hspace{1pt}dx = -\frac{1}{6}(\beta-\alpha)^3\hspace{10pt}}$$

から求めると

$$ \begin{aligned} S = & \int_{0}^{3a} (-x^2 +3ax)\hspace{1pt} dx\\[1em] =& -\int_{0}^{3a} x(x-3a)\hspace{1pt} dx\\[1em] =& -\left(-\frac{1}{6} (3a-0)^3 \right)\\[1em] =&\frac{9}{2} a^3\\[1em] \end{aligned} $$

面積\(\hspace{1pt}S\hspace{1pt}\)が\(\hspace{1pt}9\hspace{1pt}\)であることから $$ \begin{aligned} \frac{9}{2} a^3 = & 9\\[1em] a^3 =& 2\\[1em] a =& \sqrt[3]{2}\\[1em] \end{aligned} $$ となります。

したがって、放物線\(\hspace{2pt}y = -x^2 +3ax\hspace{2pt}\)\(\hspace{2pt}(a > 0)\hspace{1pt}\)と\(\hspace{1pt}x\hspace{1pt}\)軸で囲まれた部分の面積が\(\hspace{1pt}9\hspace{1pt}\)のとき、定数\(\hspace{1pt}a\hspace{1pt}\)は $${a =\sqrt[3]{2}}$$ と求められます。

【関連するページ】
・定積分

・1/6公式

　【出題範囲】　　　【難易度】


　



Copyright (c) 光学技術の基礎用語 All Rights Reserved.