放物線とx軸で囲まれた面積を直線で二等分する条件
◆第問目!
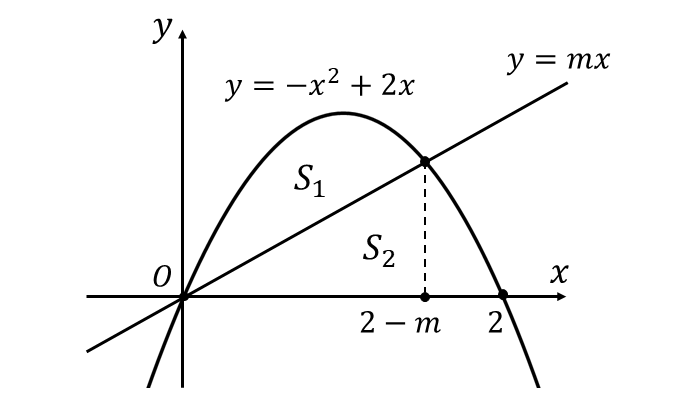
放物線\(\hspace{2pt}y = -x^2 +2x\hspace{2pt}\)と直線\(\hspace{1pt}y = mx\hspace{1pt}\)によって囲まれる面積を\(\hspace{1pt}S\hspace{1pt}\)とし、その面積のうち直線の上側を\(\hspace{1pt}S_1\)、下側を\(\hspace{1pt}S_2\hspace{1pt}\)とします。
このとき、面積\(S_2\hspace{1pt}\)は積分から面積を求めと計算量が多くなるため、 $${S = 2 S_1}$$ という式から面積の二等分を考えると計算が楽になります。
【解答のポイント】
放物線\(\hspace{2pt}y = -x^2 +2x\hspace{2pt}\)と直線\(\hspace{1pt}y = mx\hspace{1pt}\)によって囲まれる面積を\(\hspace{1pt}S\hspace{1pt}\)とし、その面積のうち直線の上側を\(\hspace{1pt}S_1\)、下側を\(\hspace{1pt}S_2\hspace{1pt}\)とします。
ここで、面積\(S_2\hspace{1pt}\)は積分から面積を求めと計算量が多くなるため、 $${S = 2 S_1}$$ という式から面積の二等分を考えると計算が楽になります。
積分の計算には、放物線と\(\hspace{1pt}x\hspace{1pt}\)軸に囲まれた面積\(\hspace{1pt}S\hspace{1pt}\)は1/6公式
を用いると簡単に計算できます。
【解答】
まず、放物線\(\hspace{2pt}y = -x^2 +2x\hspace{2pt}\)と直線\(\hspace{1pt}y = mx\hspace{1pt}\)が\(\hspace{1pt}2\hspace{1pt}\)つの異なる交点を持つ条件を求めます。
\(\hspace{2pt}y = -x^2 +2x\hspace{2pt}\)と\(\hspace{1pt}y = mx\hspace{1pt}\)の交点の\(\hspace{1pt}x\hspace{1pt}\)座標は $$\begin{aligned} -x^2 +2x & = mx \\[0.5em] x^2 -2x +mx &= 0\\[0.5em] x \{x - (2-m)\} &= 0\\[0.5em] \end{aligned} $$
よって、\(x = 0 , 2-m\hspace{1pt}\)となります。
ここで、放物線と直線が\(\hspace{1pt}2\hspace{1pt}\)つの異なる交点を持つためには、放物線と\(\hspace{1pt}x\hspace{1pt}\)軸の交点\(\hspace{1pt}x = 0,2\hspace{1pt}\)の範囲に放物線と直線の交点があればよいので
$$ 0 < 2-m < 2 $$
すなわち
$${0 < m < 2}$$
が定数\(\hspace{1pt}m\hspace{1pt}\)の条件となります。
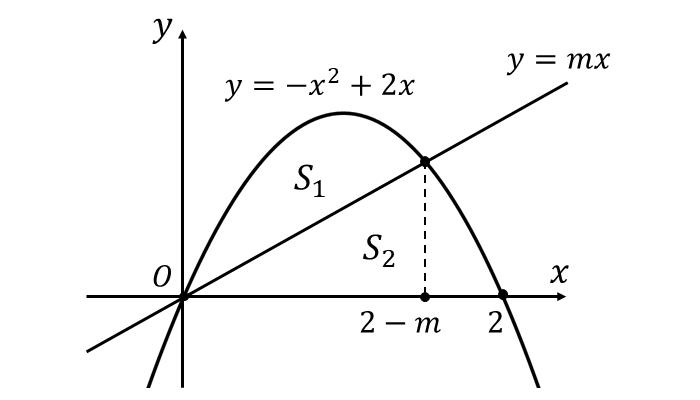
ここで、放物線と\(\hspace{1pt}x\hspace{1pt}\)軸に囲まれた面積\(\hspace{1pt}S=S_1 + S_2\hspace{1pt}\)は1/6公式
から求めると
また、放物線と直線\(\hspace{1pt}y = mx\hspace{1pt}\)に囲まれた面積\(\hspace{1pt}S_1\hspace{1pt}\)は
したがって、面積を二等分するとき $${ 2 S_1} = S $$ であることから $$ \begin{aligned} 2 \cdot \frac{1}{6} (2-m)^3 & = \frac{4}{3}\\[1em] (2-m)^3 & = 4 \\[1em] 2-m =& \sqrt[3]{4}\\[1em] m =& 2-\sqrt[3]{4} \\[1em] \end{aligned} $$
以上から、放物線\(\hspace{2pt}y = -x^2 +2x\hspace{2pt}\)と\(\hspace{1pt}x\hspace{1pt}\)軸で囲まれた部分の面積を直線\(\hspace{1pt}y = mx\hspace{1pt}\)で二等分するときの、定数\(\hspace{1pt}m\hspace{1pt}\)は $${m = 2-\sqrt[3]{4}}$$ となります。
【関連するページ】
・定積分