-光と光学に関連する用語の解説サイト-

直線と放物線に囲まれた面積

◆第問目！

【 難易度 ★ 】
　放物線\({\hspace{2pt}y=3x^2-5x+3\hspace{2pt}}\)と直線\({\hspace{2pt}y=4x-3\hspace{2pt}}\)に囲まれた面積\({S\hspace{2pt}}\)を求めよ

面積を求める問題は、グラフを描いて関数の上下関係を調べてから積分します。

また、放物線 (\({y=ax^2+bx+c}\)) と直線 (\({y=px+q}\)) の交点を\({x=\alpha,\hspace{2pt}\beta\hspace{3pt}}\) (\({\alpha < \beta\hspace{1pt}}\)) とするときに成り立つ1/6公式

$${S = \frac{|a|}{6}(\beta-\alpha)^3}$$

を利用すると計算が簡単になります。

【解答のポイント】

面積を求める問題は、まずグラフを描いて関数の上下関係を調べてから積分します。

また、放物線 (\({y=ax^2+bx+c}\)) と直線 (\({y=px+q}\)) の交点を\({x=\alpha,\hspace{2pt}\beta\hspace{3pt}}\) (\({\alpha < \beta\hspace{1pt}}\)) とするときに成り立つ1/6公式

$${S = \frac{|a|}{6}(\beta-\alpha)^3}$$

を利用すると簡単に計算することができます。(別解に記載)

【解答】

まず、放物線 \({y=3x^2-5x+3}\) と \({y=4x-3}\) の交点を求めます。

$$ \begin{aligned} \hspace{10pt} 3x^2-5x+3 & = 4x-3\\[0.5em] 3x^2 -9x + 6 & = 0 \\[0.5em] 3(x-1)(x-2) & = 0 \\[0.5em] \end{aligned} $$

つまり、交点は \({x=1\hspace{1pt},\hspace{1pt}2}\) となります。

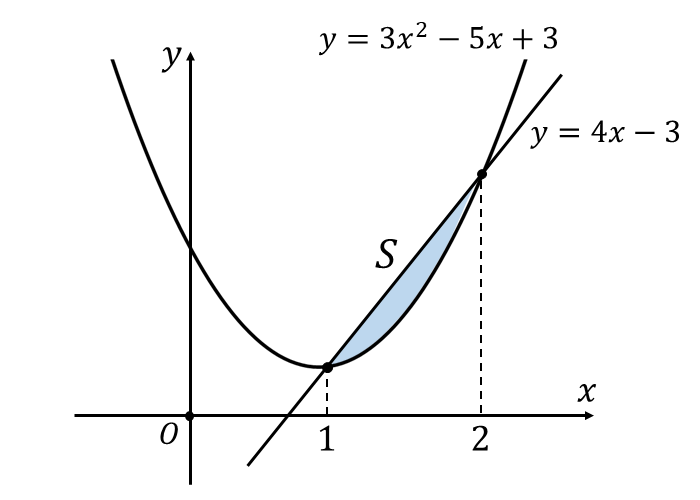
放物線 \({y=3x^2-5x+3}\) と直線 \({y=4x-3}\) に囲まれた面積を図示すると、以下のようになります。 放物線と直線に囲まれた面積を求める問題

上図から、\({1 \leqq x \leqq 2\hspace{2pt}}\)において放物線 \({y=3x^2-5x+3}\) は直線 \({y=4x-3}\) の下側に位置するため、面積\({\hspace{1pt}S\hspace{2pt}}\)は以下のように求められます。

$$ \begin{aligned} \hspace{10pt}& \int_{1}^{2} ((4x-3)-(3x^2-5x+3))\hspace{1pt} dx\\[1em] \hspace{10pt}& -3 \int_{1}^{2} (x^2-3x+2)\hspace{1pt} dx\\[1em] &=-3 \left[ \frac{1}{3}x^3 -\frac{3}{2} x^2+ 2x \right]_{1}^{2} \\[1em] &= -(2^3-1^3) + \frac{9}{2}(2^2-1^2) - 6(2-1)\hspace{10pt} \\[1em] &= -7 +\frac{27}{2} - 6\hspace{10pt} \\[1em] &= \frac{1}{2}\\[1em] \end{aligned} $$

【別解】

放物線 (\({y=ax^2+bx+c}\)) と直線 (\({y=px+q}\)) の交点を\({x=\alpha,\hspace{2pt}\beta\hspace{3pt}}\) (\({\alpha < \beta\hspace{1pt}}\)) とするときに成り立つ1/6公式

$${S = \frac{|a|}{6}(\beta-\alpha)^3}$$

から求めます。

求める面積\({\hspace{1pt}S}\) は、二次関数の二次の係数が \({a=3}\)、交点が \({x=1\hspace{1pt},\hspace{1pt}2}\) であることから $$ \begin{aligned} S &= \frac{|3|}{6}(2-1)^3 \\[1em] & = \frac{1}{2}\\[1em] \end{aligned} $$ と求められます。

【関連するページ】
・定積分

・1/6公式

　【出題範囲】　　　【難易度】


　



Copyright (c) 光学技術の基礎用語 All Rights Reserved.