√x+√y=1に囲まれた面積

【解答のポイント】

陰関数の面積を求める問題は、まず関数を変形して\({\hspace{1pt}y=\cdots\hspace{2pt}}\)の形に変形します。

次に \({x}\)軸\({\hspace{1pt},\hspace{2pt}y}\)軸 との交点を求め、グラフの概形を描きます。

最後に、定積分から面積を求めます。

【解答】

まず関数を変形して\({\hspace{1pt}y=\cdots\hspace{2pt}}\)の形に変形します。 $${\sqrt{x}+\sqrt{y}=1}$$ から $$ \begin{aligned} \sqrt{y} &=1- \sqrt{x} \\[0.5em] y & = (1-\sqrt{x})^2 \\[0.5em] & = x -2\sqrt{x}+1 \\[0.5em] \end{aligned} $$ となります。

\({x\hspace{2pt}}\)軸との交点を求めると \({y=0\hspace{2pt}}\)のとき \({\sqrt{x}=1\hspace{2pt}}\)から\({\hspace{1pt}x=1\hspace{2pt}}\)となります。

また、\({y\hspace{2pt}}\)軸との交点を求めると \({x=0\hspace{2pt}}\)のとき \({\sqrt{y}=1\hspace{2pt}}\)から\({\hspace{1pt}y=1\hspace{2pt}}\)となります。

また、グラフの傾きを求めると $${ y' = 1 -\frac{1}{\sqrt{x}} }$$ となり、\({0 < x < 1\hspace{2pt}}\)において\({\hspace{1pt}y'< 0 \hspace{2pt}}\)となることから、グラフは単調に減少するグラフになることが分かります。

以上からグラフを描くと以下のようになります。

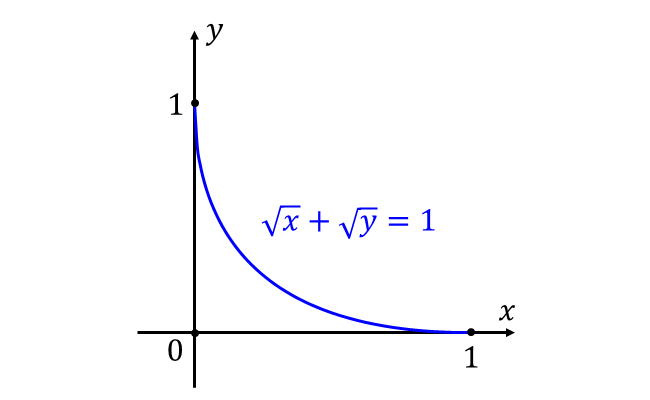
上図から、グラフに囲まれた面積は以下のように求められます。

と求められます。