-光と光学に関連する用語の解説サイト-
xy=4 と x+y=5 に囲まれた面積
◆第問目!
【 難易度 ★★ 】
\({xy=4}\) と \({x+y=5}\) に囲まれる面積を求めよ
面積を求める問題は、まずグラフの交点を求めます。
次に、囲まれる部分の関数の上下関係を調べます。
囲まれる範囲において (上側の関数)-(下側の関数) の式を作り、定積分から面積を求めます。
【解答のポイント】
まず\({\hspace{2pt}yx=4\hspace{2pt}}\)と\({\hspace{1pt}x+y=5\hspace{2pt}}\)の交点を求めます。
次に、積分する範囲において関数の上下関係を調べます。
最後に、囲まれる範囲において (上側の関数)-(下側の関数) の式を作り、定積分から面積を求めます。
【解答】
\({xy=4\hspace{2pt}}\)と\({\hspace{1pt}x+y = 5\hspace{2pt}}\)の交点を求めるために、\({y\hspace{2pt}}\)を削除します。
$$ \begin{aligned} x(5-x) &= 4 \\[1em] x^2 -5x +4&= 0 \\[1em] (x-1)(x -4) &= 0\\[1em] \end{aligned} $$すなわち \(\displaystyle{x = 1\hspace{1pt},4\hspace{2pt}}\)に交点を持ちます。
\({1 \leqq x \leqq 4\hspace{2pt}}\)の範囲において \(\displaystyle{\frac{4}{x} \leqq 5-x}\) となり、グラフは以下のようになります。
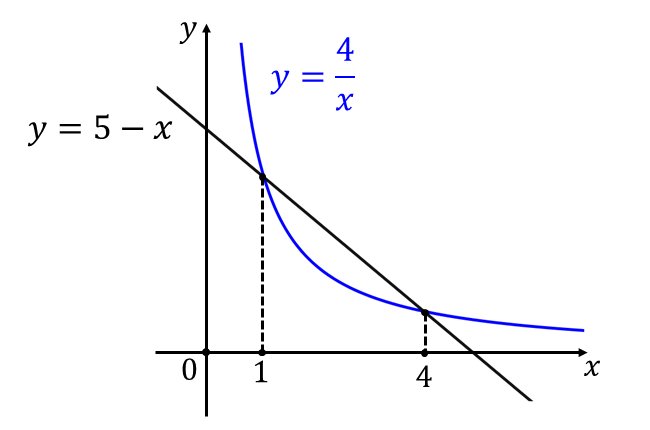
\({1 \leqq x \leqq 4\hspace{2pt}}\)において、上図の囲まれた面積を求めると、以下のようになります。
$$
\begin{aligned}
\hspace{10pt}& \int_1^{4} \left(5-x-\frac{4}{x}\right) \hspace{1pt}dx \\[1em]
&= \left[5x -\frac{1}{2}x^2 - 4\log|x| \right]_1^{4} \\[1em]
&= 5(4-1) -\frac{1}{2}(4^2-1^2) -4 (\log 4 - \log 1) \hspace{10pt}\\[1em]
&= 15 - \frac{15}{2} -4\log 2^2\\[1em]
&= \frac{15}{2} -8\log 2\\[1em]
\end{aligned}
$$
【関連するページ】
・定積分
【出題範囲】 【難易度】